Coding

Thinking in z^3

This is a quick introduction to the z^3 language (pronounced as "zcubes language").

z^3 is an easy to write, natural to read, language powered by high performance computing. Learn z^3 Language in detail by clicking this link.

• z^3 Language Detail
• z^3 Commands and Operators
• Z Functions, Member Functions, etc.

An introduction to z^3 Code Mode in ZCubes is detailed below.

Code Mode in ZCubes

To test the ZCubes platform in code mode,Visit https://code.zcubes.com

Enter code in the code editor and press run to execute. If the Browser Debugger is switched on, and if Debug button is pressed, the code inside can be debugged in the browser debugger itself.

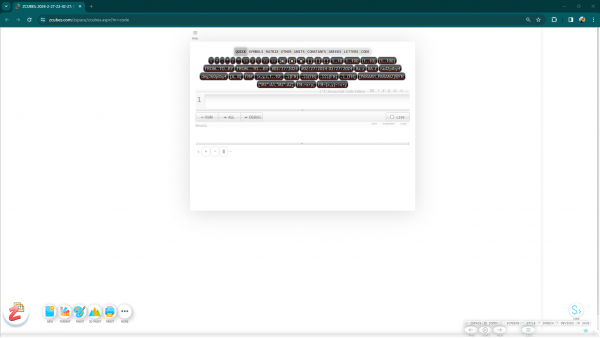
ZCubes Code Mode Control Panel

The responsive panel tabs can be used to select code segments, symbols, units, etc. and insert into the coding area. Listing of functions can be obtained by Ctrl+Space in the editor. Member functions show up on appropriate parts of the code with the same Ctrl+Space key combination.

Several of the key features are listed below, with examples. Code segments below can be copied and pasted to the ZCubes code editor to execute.

Series Comprehension

1..100..2
1...1000000...2
..40
rad2piby30
deg360by15
#a-z
MONTHS,DAYS, PLANETS
// #1/20/2024-1/20/2025

@ & Combinatorial Arguments

• Array of Functions apply to Array of Data (@)
  • Combinatorial Arguments
    • • Avoids Loops
• Functions apply Function (@)
• Easy Function Definition

1..10@SIN;
[3..10,5..10]@CHIDIST;
1..10@[SIN,COS,"x^2"];

Units & Constants

• 4m, 40ly, 45(m/s)
• %g, %c, %avo
• Seamless in Functions

%g;
%avo;
%plan;
45(m/s);
34m<*>45cm;
π;

/* energy mass equation */
units.on; // triggers array-based units calc
Energy:=mass*%c^2;
Energy(1kg)

45°<>㎭;

45℃<>℉;

units.on;
AreaOfCircle:=π*r^2;
AreaOfCircle((1..10)<>m)

Arrays, Matrices, Collections

• |x|
  • Creation
• a|x^y| b
  • Array Functions
• Array Member Functions
• Array Sensitive Functions
• Arrayfy Operator
• Related: Queues, Stacks, Graphs, Sets, Maps, etc.

|5|;
|3,4,4,1..10|;
1..10|x^2|3;
1..10|x+y^2|11..20;
SIN(1..10);
1..10.chunks(5);
1..10.parts(5);
1..10.pieces(3)

v:=u+a*t;
v ⩨;
v(0..5,3..5,6..10);
[0..5,3..5,6..10]@v

SIN(deg360by20);

a1=1..10;
a1.across(a1,SUM);

(1..100@SIN).graph()
	

Portability & Extensibility

• Multi Platform
  • Windows, Mac, Linux, Browser
• Multi-Modal
  • Browser, Desktop, CLIServer, Web-Server, IoT
• Compatibility
  • npmjs & js libraries
  • Native Interfaces
• Browser Integration
• Integrated Functionality

a=$(".zcube").length;

addsq:=a^2+b^2;

Advanced Types

• Big Numbers
• High Accuracy Floats
• Fractions
• Complex Numbers
• Array Based Computation
  • units.on;
• Render (2D and 3D)
  • Programming Media
• Symbolic Algebra

(100n)! ;
(1.3%%5)^2;
SIN(2+34i);
(3+4i)!;
SIN((1..4)+(3..4)<>i);
PI(100);

units.on;
(1/3d50)*3;

// circle around polygon points
pts=MAKEPOLYGONPOINTS(50,200)
.concat(MAKEPOLYGONPOINTS(50,100))
RENDER(
   [
      ["type","cx","cy","r","stroke","stroke-width","fill","count"],
      ["circle",i=>300+pts[i][0],i=>300+pts[i][1],100,"black",1,i=>"transparent",pts.length]
   ]
)
""

// circle around polygon points
noofpoints=50;
pts=MAKEPOLYGONPOINTS(noofpoints,[100,100],[300,300],-90)
start=pts[0];
circlesat=
	pts
		.map(
			p=>[p[0],p[1],SQRT(POWER(p[0]-start[0],2)+POWER(p[1]-start[1],2))]
		)

RENDER(
	[
		["type","cx","cy","r","stroke","stroke-width","count"],
		["circle",circlesat.column(0),circlesat.column(1),circlesat.column(2), i=>d3.interpolateInferno(i/circlesat.length) ,1,circlesat.length]
	]
)
""

Other Modes

• Browser
• CLI
• Desktop
• Server
• Web Server
• Over 100 In Production
  • Examples

Scaling Up

z^3 can be used in a variety of platforms, and for any scale of programs. The versatility of the language makes it very useful to solve intricate problems, and we hope the language may trigger everyone to think of programming logic as a natural part of intellectual activity.

Simple. Powerful. Versatile.