Manuals/calci/UNIFORM
UNIFORMDISTRIBUTED(x,ll,ul)
- is the value of the function.
- is the lower limit.
- is the upper limit of the function.
Description
- This function gives the probability of the uniform distribution.
- Uniform distribution is a symmetric probability distribution.
- It is also called rectangular distribution.
- In , is the numeric value to find the probability of the distribution, is the lower limit value and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ul } is the upper limit value.
- The Probability Density Function of the uniform distribution for the interval(a,b) is given by:
P(x)=Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} 0, &for &x<a \\ 1/b-a, &for &a<&x<b \\ 0, &for &x>b \end{cases}}
equation
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x)= \begin{cases} 0, &for &x<a \\ 1/b-a, &for &a<x<b \\ 0, &for &x>b \end{cases} }
- The Lucas numbers are defined by: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x)=\begin{cases} 0, &for &x<a \\ 1/b-a, &for &a<x<b \\ 0, &for &x>b \end{cases}}
Examples
- UNIFORMDISTRIBUTED(4,2,3) = 4030484680552036 2.6280935418326408 2.2810050058178604 2.97846262995153679
- UNIFORMDISTRIBUTED(5,3,6) = 5.522187389200553 3.566177821950987 5.04674904467538 5.301322509767488 4.9094569575972855
 is the value of the function.
is the value of the function.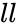 is the lower limit.
is the lower limit.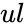 is the upper limit of the function.
is the upper limit of the function.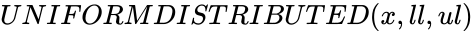 ,
,