Manuals/calci/TTESTTWOSAMPLESEQUALVARIANCES
TTESTTWOSAMPLESEQUALVARIANCES (Array1,Array2,HypothesizedMeanDifference,Alpha,NewTableFlag)
- and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array2 } are set of values.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle HypothesizedMeanDifference } is the Hypothesized Mean Difference.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Alpha } is the significance level.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NewTableFlag } is either 0 or 1.
Description
- This function calculating the two Sample for equal variances determines whether two sample means are equal.
- We can use this test when both:
- 1.The two sample sizes are equal;
- 2.It can be assumed that the two distributions have the same variance.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle TTESTTWOSAMPLESEQUALVARIANCES (Array1,Array2,HypothesizedMeanDifference,Alpha,NewTableFlag)} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array1 } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array2 } are two arrays of sample values. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle HypothesizedMeanDifference } is the Hypothesized Mean Difference .
- Suppose HypothesizedMeanDifference=0 which indicates that sample means are hypothesized to be equal.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Alpha } is the significance level which ranges from 0 to 1.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NewTableFlag } is either 0 or 1.
- "1" is indicating the result will display in new worksheet.Suppose we are omitted the NewTableFlag value it will consider the value as "0".
- The t statistic of this function calculated by:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t = \frac{\bar{x_1}-\bar{x_2}}{s_{x1}.s_{x2}.\sqrt{\frac{2}{n}}}}
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_{x1}.s_{x2} = \sqrt{\frac{1}{2}(s_{x1}^2+s_{x2}^2)}}
- Here Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_{x1}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_{x2}} are unbiased estimators of the variances of two samples.Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_{x1}.s_{x2}} is the grand standard deviation data 1 and data2 and n is the data points of two data set.
- This function will give the result as error when
1.any one of the argument is non-numeric.
2.Alpha>1
3.Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array1 }
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array2 }
are having different number of data points.
Examples
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 10 | 15 | 18 | 27 | 12 | 34 |
| 2 | 17 | 20 | 25 | 39 | 9 | 14 |
- =TTESTTWOSAMPLESEQUALVARIANCES(A1:F1,A2:F2,2,0.5,1)
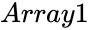 and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array2 }
are set of values.
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Array2 }
are set of values.