Manuals/calci/FTEST
FTEST(array1,array2)
- and are array of data.
Description
- This function gives the result of F-test.
- The F-test is designed to test if two population variances are equal.
- It does this by comparing the ratio of two variances.
- So, if the variances are equal, the ratio of the variances will be 1.
- Let X1,...Xn and Y1...Ym be independent samples each have a Normal Distribution .
- It's sample means:
and
- .
- The sample variances :
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle SX^2=\frac{1}{n-1} \sum_{i=1}^n (Xi-\bar X)^2}
and
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle SY^2=\frac{1}{m-1} \sum_{i=1}^m (Yi-\bar Y)^2}
- Then the Test Statistic = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac {Sx^2}{Sy^2}} has an F-distribution with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 'n−1' } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m−1} degrees of freedom.
- In FTEST(array1,array2) where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle array1} is the data of first array, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle array2} is the data of second array.
- The array may be any numbers, names, or references that contains numbers.
- values are not considered if the array contains any text, logical values or empty cells.
When the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle array1} or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle array2} is less than 2 or the variance of the array value is zero, then this function will return the result as error.
ZOS
- The syntax is to calculate FTEST in ZOS is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle FTEST(array1,array2)}
.
- and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle array2 } are array of data.
- For e.g.,FTEST([15,29,30],[62,74,80])
Examples
1.
| 15 | 27 | 19 | 32 |
| 21 | 12 | 30 | 11 |
=FTEST(B4:B8,C4:C8)=0.81524906747183
2.
| 5 | 8 | 12 | 45 | 23 |
| 10 | 20 | 30 | 40 | 50 |
=FTEST(A1:A5,C1:C5)=0.9583035732212274
3.
| 14 | 26 | 37 |
| 45 | 82 | 21 | 17 |
FTEST(B1:B3,C1:C4} = 0.26412211240525474
4.
| 14 |
| 45 | 65 |
=FTEST(B1,C2:C3)=NAN
Related Videos
See Also
References
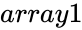 and
and 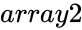 are array of data.
are array of data.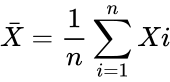 and
and
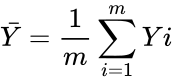 .
.