Manuals/calci/INTERCEPT
Jump to navigation
Jump to search
INTERCEPT (KnownYArray,KnownXArray)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KnownYArray} is the set of dependent data
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KnownXArray}
is the set of independent data.
- INTERCEPT(),returns the intercept of the linear regression line.
Description
- This function is calculating the point where the line is intersecting y-axis using dependent and independent variables.
- Using this function we can find the value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y } when Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x } is zero.
- The intercept point is finding using simple linear regression.
- It is fits a straight line through the set of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n } points in such a way that makes vertical distances between the points of the data set and the fitted line as small as possible.
- Regression methods nearly to the simple ordinary least squares also exist.
- i.e.,The Least Squares method relies on taking partial derivatives with respect to the slope and intercept which provides a solvable pair of equations called normal equations.
- Suppose there are Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n } data points Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {y_{i}, x_{i}}} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i = 1, 2,...n}
- To find the equation of the regression line:Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a=\bar{y}-b.\bar{x}} .
- This equation will give a "best" fit for the data points.
- The "best" means least-squares method. Here b is the slope.
- The slope is calculated by:Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b=\frac{\sum_{i=1}^{n} {(x_{i}-\bar{x})(y_{i}-\bar{y})}} {\sum_{i=1}^{n}{(x_{i}-\bar{x})}^2}} .
- In this formulaFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{x}} andFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{y}} are the sample means AVERAGE of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} and .
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle INTERCEPT (KnownYArray,KnownXArray)} , the arguments can be numbers, names, arrays, or references that contain numbers.
- The arrays values are disregarded when it is contains text, logical values or empty cells.
- This function will return the result as error when any one of the argument is non-numeric or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} is having different number of data points and there is no data.
ZOS
- The syntax is to calculate intercept of the regression line in ZOS is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle INTERCEPT (KnownYArray,KnownXArray)}
.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KnownYArray} is the set of dependent data
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KnownXArray} is the set of independent data.
- For e.g.,intercept([14,16,19,15.25],[20.1,26,10,26.4])
Examples
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | 4 | 5 | 2 | 10 | |
| 2 | 12 | 20 | 15 | 11 | |
| 3 | 25 | -12 | -9 | 30 | 18 |
| 4 | 10 | 15 | -40 | 52 | 36 |
- =INTERCEPT(A1:D1,A2:D2)= 10.13265306
- =INTERCEPT(A3:E3,A4:E4)= 4.754939085
Related Videos
See Also
References
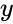 .
.