Manuals/calci/FISHERINV
Jump to navigation
Jump to search
FISHERINV(Number)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Number}
is the value to find inverse of fisher transformation.
- FISHERINV(), returns the inverse of the Fisher transformation.
Description
- This function gives the inverse of the Fisher transformation.
- We use this to test the correlations between set of data.
- The Inverse of the Fisher transformation is: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x= \frac {e^{2y-1}}{e^{2y+1}}} i.e Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=FISHER(x)} , then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle FISHERINV(y)=x}
- It can be used to construct a confidence interval.
- A confidence interval (CI) is a type of interval estimate of a population parameter and is used to indicate the reliability of an estimate.
This function will give the result as error when the value is non-numeric.
ZOS
- The syntax is to calculate FISHERINV in ZOS is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle FISHERINV(Number)}
.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Number} is the value to find inverse of fisher transformation.
- For e.g.,FISHERINV(0.4521..0.507..0.01)
Examples
- FISHERINV(0.6389731838) = 0.56419999998
- FISHERINV(0) = 0
- FISHERINV(0.1234) = 0.1227774315035342
- FISHERINV(1) = 0.761594155955765
- FISHERINV(-0.4296) = -0.4049869686465480
Related Videos
See Also
References
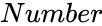 value is non-numeric.
value is non-numeric.