IMEXP(z)
- where is the complex number.
Description
- This function gives the exponential of a complex number.
- In , , & are real numbers & is the imaginary unit. .
- Euler's formula states that is the base of the natural logarithm.
- The approximate value of the constant e=2.718281828459045 and it is equal to . So the exponential of a complex number is : .
- When imaginary part is '0', it will give the exponent value of the real number. *i.e.IMEXP(z)=EXP(z) when imaginary number (iy) is '0'.
- We can use COMPLEX function to convert the real and imaginary coefficients to a complex number.
Examples
- IMEXP("2+3i")=-7.315110094901102+1.0427436562359i
- IMEXP("4-5i")=15.4874305606508+52.355491418482i
- IMEXP("6")=403.428793492735
- IMEXP("2i")=-0.416146836547142+0.909297426825682i
- IMEXP("0")=1 andIMEXP("0i")=1
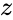 is the complex number.
is the complex number.