Manuals/calci/IMPOWER
IMPOWER(z,n)
- is the complex number is of the form
- is the power value.
Description
- This function gives the value of powers of complex number.
- DeMoivre's Theorem is a generalized formula to compute powers of a complex number in it's polar form.
- i'is the imaginary unit,
- Then the power of a complex number is defined by Failed to parse (syntax error): {\displaystyle (z)^n=(x+iy)^n=r^n*e^{inθ}=r^n(cosnθ+isinnθ)} where . and Failed to parse (syntax error): {\displaystyle θ=tan^-1(y/x)} , θ∈(is belongs to) (-Pi(),Pi()].
- This formula is called DeMoivre's theorem of complex numbers.
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
- In IMPOWER(z,n), n can be integer, fractional or negative.
- suppose n is nonnumeric , this function will returns the error value.
Examples
- IMPOWER("4+5i",3)=-235.99999+115i
- IMPOWER("9-7i",4)=-14852-8063.999999i
- IMPOWER("6",9)=10077696(EXCEL)=10077696-8i(CALCI)
- IMPOWER("i",10)=-1-16i(CALCI)=-1+6.1257422745431E-16i
- For imaginary value '0' is not accepting in CALCI.
See Also
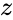 is the complex number is of the form
is the complex number is of the form 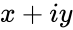
 is the power value.
is the power value.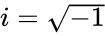
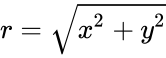 . and Failed to parse (syntax error): {\displaystyle θ=tan^-1(y/x)}
, θ∈(is belongs to) (-Pi(),Pi()].
. and Failed to parse (syntax error): {\displaystyle θ=tan^-1(y/x)}
, θ∈(is belongs to) (-Pi(),Pi()].