BARTLETTSTEST(DataRange,ConfidenceLevel,NewTableFlag)
- is the array of x values.
- is the value from 0 to 1.
- is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.
Description
- Bartlett's test is used to test if k samples are from populations with equal variances.
- Also called Bartlett's test for homogeneity of variances. It is used to test if variances are equal for all samples.
- Bartlett's test is sensitive to departures from normality.
- It is used when you’re fairly certain your data comes from a normal distribution.
- That is, if the samples come from non-normal distributions, then Bartlett's test may simply be testing for non-normality.
- B is the Bartlett's test static.
- is the pooled variance across all groups.
Result
- If p-value is greater than BCriticl value, reject the null hypothesis.
- Else retain null hypothesis.
Example
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 51 | 82 | 79 | 85 |
| 2 | 87 | 91 | 84 | 80 |
| 3 | 50 | 92 | 74 | 65 |
| 4 | 48 | 80 | 98 | 71 |
| 5 | 79 | 52 | 63 | 67 |
| 6 | 61 | 79 | 83 | 51 |
| 7 | 53 | 73 | 85 | 63 |
| 8 | 54 | 74 | 58 | 93 |
=BARTLETTSTEST([A1:A8,B1:B8,C1:C8,D1:D8],0.05,true)
| DATA-0 | DATA-1 | DATA-2 | DATA-3 | |
|---|---|---|---|---|
| MEAN | 60.375 | 77.875 | 78 | 71.875 |
| VARIANCE | 214.26785714285714 | 157.55357142857142 | 164.57142857142858 | 181.55357142857142 |
| LNVARIANCE | 5.367226901229239 | 5.059765536486956 | 5.1033446922005234 | 5.201550769540011 |
| COUNT | 8 | 8 | 8 | 8 |
| DF | 7 | 7 | 7 | 7 |
| 1/DF | 0.14285714285714285 | 0.14285714285714285 | 0.14285714285714285 | 0.14285714285714285 |
| SAMPLE DATA | |
|---|---|
| DF | 28 |
| 1/DF | 0.03571428571428571 |
| VARIANCE | 179.48660714285714 |
| LNVARIANCE | 5.19010059312721 |
| DATA | |
|---|---|
| B-NUMERATOR | 0.19960131136474502 |
| B-DENOMINATOR | 1.0595238095238095 |
| B | 0.18838775454650092 |
| P-VALUE | 0.979441777737987 |
| B-CRITICAL | 7.810299999999978 |
| RESULT | THE P-VALUE IS LESSER THAN THE B-CRITICAL VALUE, SO THE VARIANCES ARE JUDGED TO BE EQUAL. |
See Also
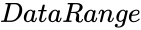 is the array of x values.
is the array of x values.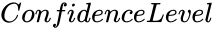 is the value from 0 to 1.
is the value from 0 to 1.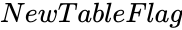 is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.
is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.