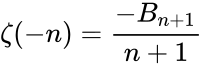Difference between revisions of "Manuals/calci/RIEMANNZETA"
Jump to navigation
Jump to search
| (8 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''RIEMANNZETA(s)'''</div><br/> | <div style="font-size:30px">'''RIEMANNZETA(s)'''</div><br/> | ||
| − | *<math>s</math> is the value from 0 | + | *<math>s</math> is the value from <math>0</math> to <math>infinity</math>. |
==Description== | ==Description== | ||
| Line 7: | Line 7: | ||
*This function is useful in number theory for the investigating properties of prime numbers. | *This function is useful in number theory for the investigating properties of prime numbers. | ||
*It is denoted by <math>\zeta(s)</math>. | *It is denoted by <math>\zeta(s)</math>. | ||
| − | *This function is defined as the infinite series | + | *This function is defined as the infinite series <math>\zeta(s)=1+2^{-s}+3^{-s}+.....</math>. |
*When the value of s=1,then this series is called the harmonic series. | *When the value of s=1,then this series is called the harmonic series. | ||
*When it is increase without any bound or limit, then its sum is infinite. | *When it is increase without any bound or limit, then its sum is infinite. | ||
*When the value of s is larger than 1,the the series converges to a finite number as successive terms are added. | *When the value of s is larger than 1,the the series converges to a finite number as successive terms are added. | ||
*The riemann zeta function is defined for Complex numbers also. | *The riemann zeta function is defined for Complex numbers also. | ||
| − | *So | + | *So <math>\zeta(s)</math> is a function of a complex variable <math>s = \sigma + it</math>,where <math>\sigma</math> and t are real numbers.i is the imaginary unit. |
| − | *It is a function of a complex variable s that analytically continues the sum of the infinite series , which converges when the real part of s is greater than 1. | + | *It is also a function of a complex variable s that analytically continues the sum of the infinite series , which converges when the real part of s is greater than 1. |
| − | *It is defined by : | + | *It is defined by :<math>\zeta(s)=\sum_{n=1}^\infty n^{-s}= \frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+.....</math> where <math>\sigma</math> =Real part of s>1. |
| − | *We can define this by integral also: | + | *We can define this by integral also:<math>\zeta(s)=\frac{1}{\Gamma(s)} \int\limits_{0}^{\infty}\frac{x^{s-1}}{e^{x-1}}\,dx </math> |
*Riemann zeta function is a meromorphic function on the whole complex s-plane, which is holomorphic everywhere except for a simple pole at s = 1 with residue 1. | *Riemann zeta function is a meromorphic function on the whole complex s-plane, which is holomorphic everywhere except for a simple pole at s = 1 with residue 1. | ||
| − | * | + | *For special values: |
| + | *(i)Any positive integer 2n. | ||
| + | :<math>\zeta(2n)=\frac{(-1)^{n+1}B_{2n}(2\pi)^{2n}}{2(2n)!}</math> where <math>B_{2n}</math> is a Bernoulli number. | ||
| + | *(ii)For negative integers: | ||
| + | :<math>\zeta(-n)=\frac{-B_{n+1}}{n+1}</math> | ||
| + | *For n ≥ 1,so in particular ζ vanishes at the negative even integers because Bm = 0 for all odd m other than 1. | ||
*For odd positive integers, no such simple expression is known. | *For odd positive integers, no such simple expression is known. | ||
**When s=1,then ζ (1) is Harmonic series. | **When s=1,then ζ (1) is Harmonic series. | ||
**when s=2, then ζ (2) derivation is Basel problem. | **when s=2, then ζ (2) derivation is Basel problem. | ||
**when s=3, then ζ (3) derivation is Apery's constant. | **when s=3, then ζ (3) derivation is Apery's constant. | ||
| − | **When s=4, then ζ (4) derivation is Planck's law | + | **When s=4, then ζ (4) derivation is Planck's law. |
| + | |||
| + | ==Examples== | ||
| + | #=RIEMANNZETA(0)= -1/2 | ||
| + | #=RIEMANNZETA(4) = π^4/90 | ||
| + | #=RIEMANNZETA(-25)= -657931/12. | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|ZlYfEqdlhk0|280|center|Zeta Function}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/LEVENESTEST| LEVENESTEST]] | ||
| + | *[[Manuals/calci/MOODSMEDIANTEST| MOODSMEDIANTEST]] | ||
| + | *[[Manuals/calci/FRIEDMANTEST| FRIEDMANTEST]] | ||
| + | *[[Manuals/calci/KSTESTNORMAL| KSTESTNORMAL]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Riemann_zeta_function Riemann Zeta Function] | ||
Latest revision as of 15:22, 18 July 2015
RIEMANNZETA(s)
- is the value from to .
Description
- This function gives the result for the function of Riemann-Zeta function.
- It is also known as Euler-Riemann Zeta function.
- This function is useful in number theory for the investigating properties of prime numbers.
- It is denoted by .
- This function is defined as the infinite series .
- When the value of s=1,then this series is called the harmonic series.
- When it is increase without any bound or limit, then its sum is infinite.
- When the value of s is larger than 1,the the series converges to a finite number as successive terms are added.
- The riemann zeta function is defined for Complex numbers also.
- So is a function of a complex variable ,where and t are real numbers.i is the imaginary unit.
- It is also a function of a complex variable s that analytically continues the sum of the infinite series , which converges when the real part of s is greater than 1.
- It is defined by : where =Real part of s>1.
- We can define this by integral also:
- Riemann zeta function is a meromorphic function on the whole complex s-plane, which is holomorphic everywhere except for a simple pole at s = 1 with residue 1.
- For special values:
- (i)Any positive integer 2n.
- where is a Bernoulli number.
- (ii)For negative integers:
- For n ≥ 1,so in particular ζ vanishes at the negative even integers because Bm = 0 for all odd m other than 1.
- For odd positive integers, no such simple expression is known.
- When s=1,then ζ (1) is Harmonic series.
- when s=2, then ζ (2) derivation is Basel problem.
- when s=3, then ζ (3) derivation is Apery's constant.
- When s=4, then ζ (4) derivation is Planck's law.
Examples
- =RIEMANNZETA(0)= -1/2
- =RIEMANNZETA(4) = π^4/90
- =RIEMANNZETA(-25)= -657931/12.
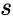 is the value from
is the value from 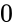 to
to 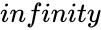 .
.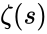 .
.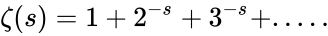 .
. ,where
,where  and t are real numbers.i is the imaginary unit.
and t are real numbers.i is the imaginary unit.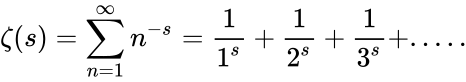 where
where 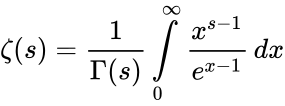
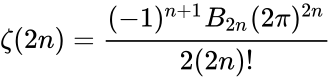 where
where 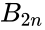 is a Bernoulli number.
is a Bernoulli number.