Manuals/calci/INTEGERDIVISION
Jump to navigation
Jump to search
INTEGERDIVISION (Numerator,Denominator)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Numerator} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Denominator} are any positive real numbers.
Description
- This function returns the quotient of the division.
- The result of the quotient will be in Integer part only.
- Division is one of the four basic operations of arithmetic.
- Division is splitting into equal parts or groups.
- Division is the repeated subtraction and it is the opposite of Multiplication.
- The division of two natural numbers is the process of calculating the number of times one number is contained within one another.
- In , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Numerator} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Denominator} are any positive real numbers.
- Numerator is the dividend and denominator is the divisor.
- This function will return the result as error when the denominator is in negative number.
Examples
- INTEGERDIVISION(9,4) = 2
- INTEGERDIVISION(873,19) = 45
- INTEGERDIVISION(1652,87.24) = 18
- INTEGERDIVISION(-6541,-124.005) = 52
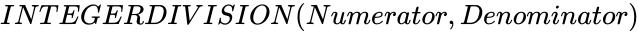 , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Numerator}
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Denominator}
are any positive real numbers.
, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Numerator}
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Denominator}
are any positive real numbers.