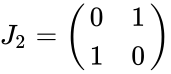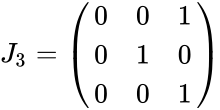Difference between revisions of "Manuals/calci/EXCHANGE"
Jump to navigation
Jump to search
| Line 58: | Line 58: | ||
| 1 || 0 || 0 || 0 || 0 || 0 | | 1 || 0 || 0 || 0 || 0 || 0 | ||
|} | |} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/HADAMARD| HADAMARD]] | ||
| + | *[[Manuals/calci/HESSENBERG| HESSENBERG]] | ||
| + | *[[Manuals/calci/IDENTITY| IDENTITY]] | ||
| + | *[[Manuals/calci/HANKEL| HANKEL]] | ||
| + | |||
| + | ==References== | ||
Revision as of 10:04, 27 April 2015
MATRIX("EXCHANGE",order)
- is the order of the Exchange matrix.
Description
- This function gives the exchange matrix of order 3.
- The exchange matrix is the square matrix of a permutation matrix.
- In this matrix the 1 elements reside on the counterdiagonal and all other elements are zero.
- It is a 'row-reversed' or 'column-reversed' version of the identity matrix.
- Suppose J is an nxn exchange matrix, then the elements of J are defined such that
.
- It is also called the reversal matrix,backward identity, or standard involutory permutation.
- The form of exchange matrices are
Examples
- 1.MATRIX("Exchange")
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
- 2.MATRIX("Exchange",6)
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 |
 is the order of the Exchange matrix.
is the order of the Exchange matrix.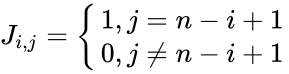 .
.