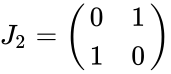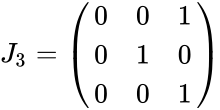Difference between revisions of "Manuals/calci/EXCHANGE"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''EXCHANGE'''</div><br/>") |
|||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''EXCHANGE'''</div><br/> | + | <div style="font-size:30px">'''MATRIX("EXCHANGE",order)'''</div><br/> |
| + | *<math>order</math> is the order of the Exchange matrix. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives the exchange matrix of order 3. | ||
| + | *The exchange matrix is the square matrix of a permutation matrix. | ||
| + | *In this matrix the 1 elements reside on the counterdiagonal and all other elements are zero. | ||
| + | *It is a 'row-reversed' or 'column-reversed' version of the identity matrix. | ||
| + | * Suppose J is an nxn exchange matrix, then the elements of J are defined such that | ||
| + | <math> J_{i,j}=\begin{cases} | ||
| + | 1, j=n-i+1 \\ | ||
| + | 0, j\neq n-i+1 \\ | ||
| + | \end{cases}</math>. | ||
| + | *It is also called the reversal matrix,backward identity, or standard involutory permutation. | ||
| + | *The form of exchange matrices are | ||
| + | <math>J_2=\begin{pmatrix} | ||
| + | 0 & 1 \\ | ||
| + | 1 & 0 | ||
| + | \end{pmatrix}</math> | ||
| + | <math>J_3=\begin{pmatrix} | ||
| + | 0 & 0 & 1 \\ | ||
| + | 0 & 1 & 0 \\ | ||
| + | 0 & 0 & 1 | ||
| + | \end{pmatrix}</math> | ||
| + | <math> J_n =\begin{pmatrix} | ||
| + | 0 & 0 & \cdots & 0 & 0 & 1 \\ | ||
| + | 0 & 0 & \cdots & 0 & 1 & 0 \\ | ||
| + | 0 & 0 & \cdots & 1 & 0 & 0 \\ | ||
| + | \vdots & \ddots & \vdots \\ | ||
| + | 0 & 1 & \cdots & 0 & 0 & 0 \\ | ||
| + | 1 & 0 & \cdots & 0 & 0 & 0 \\ | ||
| + | \end{pmatrix}</math> | ||
| + | |||
| + | |||
| + | ==Examples== | ||
| + | *1.MATRIX("Exchange") =1 | ||
| + | *2.MATRIX("Exchange",3) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 0 || 0 || 1 | ||
| + | |- | ||
| + | | 0 || 1 || 0 | ||
| + | |- | ||
| + | | 1|| 0 || 0 | ||
| + | |} | ||
| + | *3.MATRIX("Exchange",6) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 0 || 0 || 0 || 0 || 0 || 1 | ||
| + | |- | ||
| + | | 0 || 0 || 0 || 0 || 1 || 0 | ||
| + | |- | ||
| + | | 0 || 0 || 0 || 1 || 0 || 0 | ||
| + | |- | ||
| + | | 0 || 0 || 1 || 0 || 0 || 0 | ||
| + | |- | ||
| + | | 0 || 1 || 0 || 0 || 0 || 0 | ||
| + | |- | ||
| + | | 1 || 0 || 0 || 0 || 0 || 0 | ||
| + | |} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/HADAMARD| HADAMARD]] | ||
| + | *[[Manuals/calci/HESSENBERG| HESSENBERG]] | ||
| + | *[[Manuals/calci/IDENTITY| IDENTITY]] | ||
| + | *[[Manuals/calci/HANKEL| HANKEL]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Exchange_matrix Exchange matrix] | ||
Latest revision as of 00:45, 26 October 2015
MATRIX("EXCHANGE",order)
- is the order of the Exchange matrix.
Description
- This function gives the exchange matrix of order 3.
- The exchange matrix is the square matrix of a permutation matrix.
- In this matrix the 1 elements reside on the counterdiagonal and all other elements are zero.
- It is a 'row-reversed' or 'column-reversed' version of the identity matrix.
- Suppose J is an nxn exchange matrix, then the elements of J are defined such that
.
- It is also called the reversal matrix,backward identity, or standard involutory permutation.
- The form of exchange matrices are
Examples
- 1.MATRIX("Exchange") =1
- 2.MATRIX("Exchange",3)
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
- 3.MATRIX("Exchange",6)
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 |
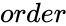 is the order of the Exchange matrix.
is the order of the Exchange matrix.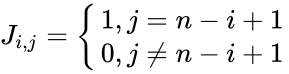 .
.