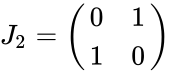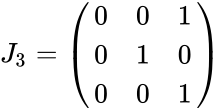Difference between revisions of "Manuals/calci/EXCHANGE"
Jump to navigation
Jump to search
| Line 34: | Line 34: | ||
==Examples== | ==Examples== | ||
| − | *1.MATRIX("Exchange") | + | *1.MATRIX("Exchange") =1 |
| + | *2.MATRIX("Exchange",3) | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 43: | Line 44: | ||
| 1|| 0 || 0 | | 1|| 0 || 0 | ||
|} | |} | ||
| − | * | + | *3.MATRIX("Exchange",6) |
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
Latest revision as of 00:45, 26 October 2015
MATRIX("EXCHANGE",order)
- is the order of the Exchange matrix.
Description
- This function gives the exchange matrix of order 3.
- The exchange matrix is the square matrix of a permutation matrix.
- In this matrix the 1 elements reside on the counterdiagonal and all other elements are zero.
- It is a 'row-reversed' or 'column-reversed' version of the identity matrix.
- Suppose J is an nxn exchange matrix, then the elements of J are defined such that
.
- It is also called the reversal matrix,backward identity, or standard involutory permutation.
- The form of exchange matrices are
Examples
- 1.MATRIX("Exchange") =1
- 2.MATRIX("Exchange",3)
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
- 3.MATRIX("Exchange",6)
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 |
 is the order of the Exchange matrix.
is the order of the Exchange matrix.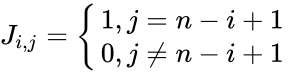 .
.