Difference between revisions of "Manuals/calci/TTESTTWOSAMPLESEQUALVARIANCES"
Jump to navigation
Jump to search
| Line 24: | Line 24: | ||
2.Alpha>1 | 2.Alpha>1 | ||
3.<math>Array1 </math> and <math> Array2 </math> are having different number of data points. | 3.<math>Array1 </math> and <math> Array2 </math> are having different number of data points. | ||
| + | |||
| + | ==Examples== | ||
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !! C !! D!! E !! F | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 10 || 15 || 18 || 27 || 12 || 34 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 17 || 20 || 25 || 39 || 9 || 14 | ||
| + | |} | ||
| + | |||
| + | #=TTESTTWOSAMPLESEQUALVARIANCES(A1:F1,A2:F2,2,0.5,1) | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/TTEST | TTEST ]] | ||
| + | *[[Manuals/calci/TDIST | TDIST ]] | ||
| + | *[[Manuals/calci/TINV | TINV ]] | ||
| + | *[[Manuals/calci/TTESTUNEQUALVARIANCES | TTESTUNEQUALVARIANCES ]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Student%27s_t-test Student's t-distribution] | ||
Revision as of 16:36, 20 December 2016
TTESTTWOSAMPLESEQUALVARIANCES (Array1,Array2,HypothesizedMeanDifference,Alpha,NewTableFlag)
- and are set of values.
- is the Hypothesized Mean Difference.
- is the significance level.
- is either 0 or 1.
Description
- This function calculating the two Sample for equal variances determines whether two sample means are equal.
- We can use this test when both:
- 1.The two sample sizes are equal;
- 2.It can be assumed that the two distributions have the same variance.
- In , and are two arrays of sample values. is the Hypothesized Mean Difference .
- Suppose HypothesizedMeanDifference=0 which indicates that sample means are hypothesized to be equal.
- is the significance level which ranges from 0 to 1.
- is either 0 or 1.
- "1" is indicating the result will display in new worksheet.Suppose we are omitted the NewTableFlag value it will consider the value as "0".
- The t statistic of this function calculated by:
where
- Here and are unbiased estimators of the variances of two samples. is the grand standard deviation data 1 and data2 and n is the data points of two data set.
- This function will give the result as error when
1.any one of the argument is non-numeric. 2.Alpha>1 3. and are having different number of data points.
Examples
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 10 | 15 | 18 | 27 | 12 | 34 |
| 2 | 17 | 20 | 25 | 39 | 9 | 14 |
- =TTESTTWOSAMPLESEQUALVARIANCES(A1:F1,A2:F2,2,0.5,1)
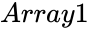 and
and 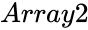 are set of values.
are set of values.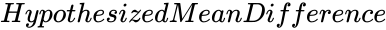 is the Hypothesized Mean Difference.
is the Hypothesized Mean Difference.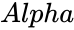 is the significance level.
is the significance level.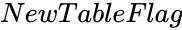 is either 0 or 1.
is either 0 or 1.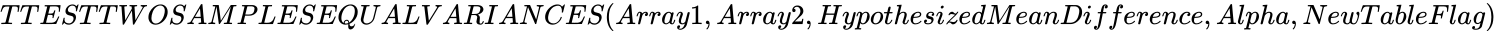 ,
, 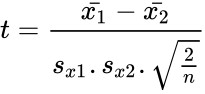
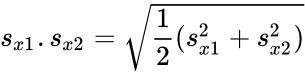
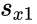 and
and 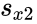 are unbiased estimators of the variances of two samples.
are unbiased estimators of the variances of two samples.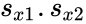 is the grand standard deviation data 1 and data2 and n is the data points of two data set.
is the grand standard deviation data 1 and data2 and n is the data points of two data set.