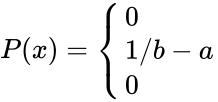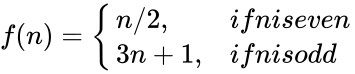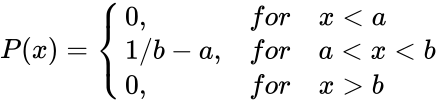Difference between revisions of "Manuals/calci/UNIFORM"
Jump to navigation
Jump to search
| Line 13: | Line 13: | ||
<math>P(x)= | <math>P(x)= | ||
\begin{cases} | \begin{cases} | ||
| − | 0 | + | 0 \\ |
| − | 1/b-a | + | 1/b-a \\ |
| − | 0 | + | 0 |
\end{cases}</math> | \end{cases}</math> | ||
| Line 22: | Line 22: | ||
n/2, &if n is even \\ | n/2, &if n is even \\ | ||
3n+1, &if n is odd | 3n+1, &if n is odd | ||
| + | \end{cases}</math> | ||
| + | |||
| + | <math>P(x)= | ||
| + | \begin{cases} | ||
| + | 0, &for &x<a \\ | ||
| + | 1/b-a, &for &a<x<b \\ | ||
| + | 0, &for &x>b | ||
\end{cases}</math> | \end{cases}</math> | ||
Revision as of 23:42, 10 February 2014
UNIFORMDISTRIBUTED(x,ll,ul)
- is the value of the function.
- is the lower limit.
- is the upper limit of the function.
Description
- This function gives the probability of the uniform distribution.
- Uniform distribution is a symmetric probability distribution.
- It is also called rectangular distribution.
- In , is the numeric value to find the probability of the distribution, is the lower limit value and is the upper limit value.
- The probability density function of the uniform distribution in the interval [a,b] are :
Examples
- UNIFORMDISTRIBUTED(4,2,3) = 4030484680552036 2.6280935418326408 2.2810050058178604 2.97846262995153679
- UNIFORMDISTRIBUTED(5,3,6) = 5.522187389200553 3.566177821950987 5.04674904467538 5.301322509767488 4.9094569575972855
 is the value of the function.
is the value of the function.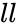 is the lower limit.
is the lower limit.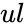 is the upper limit of the function.
is the upper limit of the function.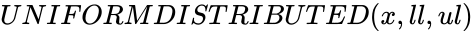 ,
,