Manuals/calci/MATRIXSYMMETRIC
Jump to navigation
Jump to search
MATRIXSYMMETRIC (GeneratedMatrix,About)
- is any matrix.
Description
- This function shows the symmetric value of the given matrix.
- In , is any matrix.
- A matrix is said to be symmetric if .
- is the transpose of the matrix A.
- Normally equal matrices have equal dimensions, only square matrices can be symmetric.
- But using this function we can get the symmetric matrix even non square matrix also.
- Consider the matrix .
- So Symmetric matrix entries are .
- The properties of symmetric matrices are:
1. Every square diagonal matrix is symmetric, since all off-diagonal entries are zero. 2. Similarly, each diagonal element of a skew-symmetric matrix must be zero, since each is its own negative. 3. Hermitian matrices are a useful generalization of symmetric matrices for complex matrices.
Examples
1. MATRIXSYMMETRIC([12,16,20;98,76,56;34,54,28])
| 12 | 98 | 20 |
| 98 | 76 | 56 |
| 20 | 56 | 28 |
2. MATRIXSYMMETRIC([[2,17,18,-34,98],[60,3.15,36,23,13],[54,55,3,19,25],[65,45,77,-90,88.8]])
| 2 | 60 | 54 | -34 | 98 |
| 60 | 3.15 | 55 | 23 | 13 |
| 54 | 55 | 3 | 19 | 25 |
| -34 | 23 | 19 | -90 | 88.8 |
 is any matrix.
is any matrix.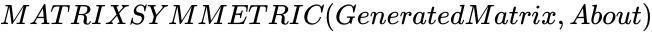 ,
,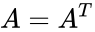 .
.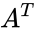 is the transpose of the matrix A.
is the transpose of the matrix A.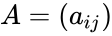 .
. .
.