Difference between revisions of "Manuals/calci/IMARGUMENT"
| (3 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''IMARGUMENT(Complexnumber)'''</div><br/> | <div style="font-size:30px">'''IMARGUMENT(Complexnumber)'''</div><br/> | ||
*<math>Complexnumber</math> is of the form <math>z=x+iy</math>. | *<math>Complexnumber</math> is of the form <math>z=x+iy</math>. | ||
| + | **IMARGUMENT(), returns the argument theta, an angle expressed in radians | ||
==Description== | ==Description== | ||
| Line 26: | Line 27: | ||
#IMARGUMENT("2") = 0 | #IMARGUMENT("2") = 0 | ||
#IMARGUMENT("4i") = 1.5707963267948966 | #IMARGUMENT("4i") = 1.5707963267948966 | ||
| − | #DEGREES(IMARGUMENT("2+2i")) = | + | #DEGREES(IMARGUMENT("2+2i")) = 45° |
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|FwuPXchH2rA|280|center|Complex Number Analysis}} | ||
==See Also== | ==See Also== | ||
| Line 35: | Line 40: | ||
==References== | ==References== | ||
*[http://mathworld.wolfram.com/ComplexArgument.html Complex Argument] | *[http://mathworld.wolfram.com/ComplexArgument.html Complex Argument] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 03:18, 23 October 2020
IMARGUMENT(Complexnumber)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Complexnumber}
is of the form .
- IMARGUMENT(), returns the argument theta, an angle expressed in radians
Description
- This function gives the principal value of an argument of a complex-valued expression Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} .
- i.e The angle from the positive axis to the line segment is called the Argument of a complex number.
- In this function angle value is in Radians.
- Here Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IMARGUMENT(Complexnumber)} , Where Complexnumber in the form of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=x+iy} . i.e Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} & Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} are the real numbers.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I} imaginary unit .Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=\sqrt{-1}} .
- An argument of the complex number Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = x + iy} is any real quantity Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} such that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = x + i y} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r cos(\phi) + i r sin(\phi)} for some positive real number Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} .
- Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r = |z| = \sqrt{x^2+y^2}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi \in (-\pi,\pi]} .
- The argument of a complex number is calculated by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle arg(z)= tan^{-1}(\frac{y}{x}) =\theta} in Radians.
- To change the Radian value to Degree we can use DEGREES function or we can multiply the answer with .
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
ZOS
- The syntax is to calculate argument of a complex number in ZOS is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IMARGUMENT(Complexnumber)}
.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Complexnumber} is of the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=x+iy} .
- For e.g.,IMARGUMENT("6.72+1.5i")
Examples
- IMARGUMENT("3-2i") = -0.5880026035475675
- IMARGUMENT("5+6i") = 0.8760580505981934
- IMARGUMENT("2") = 0
- IMARGUMENT("4i") = 1.5707963267948966
- DEGREES(IMARGUMENT("2+2i")) = 45°
Related Videos
See Also
References
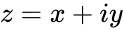 .
.