Difference between revisions of "Manuals/calci/IMSUB"
Jump to navigation
Jump to search
| Line 7: | Line 7: | ||
*IMSUB(z1,z2), Where <math> z1,z2</math> are the complex number is of the form <math>a+ib</math>. | *IMSUB(z1,z2), Where <math> z1,z2</math> are the complex number is of the form <math>a+ib</math>. | ||
*<math> a </math>& <math>b</math> are the real numbers. <math>i</math> imaginary unit .<math>i=\sqrt{-1}</math>. | *<math> a </math>& <math>b</math> are the real numbers. <math>i</math> imaginary unit .<math>i=\sqrt{-1}</math>. | ||
| − | * Let <math>z1=a+ib</math> and < | + | * Let <math>z1=a+ib</math> and <math>z2=c+id</math>. |
*The difference of two complex number is:<math>(a+ib)-(c+id)=(a-c)+(b-d)i </math> where <math>a,b,c</math> and <math>d</math> are real numbers. | *The difference of two complex number is:<math>(a+ib)-(c+id)=(a-c)+(b-d)i </math> where <math>a,b,c</math> and <math>d</math> are real numbers. | ||
*We can use COMPLEX function to convert real and imaginary number in to a complex number. | *We can use COMPLEX function to convert real and imaginary number in to a complex number. | ||
Revision as of 22:36, 25 December 2013
IMSUB(z1,z2)
- are the complex numbers is of the form
Description
- This function gives the difference of the two complex numbers.
- IMSUB(z1,z2), Where are the complex number is of the form .
- & are the real numbers. imaginary unit ..
- Let and .
- The difference of two complex number is: where and are real numbers.
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
Examples
- IMSUB("6+4i","5+3i")=1+1i
- IMSUB("3+4i","6+7i")=-3-3i
- IMSUB("8","9+10i")=-1-10i
- IMSUB("5+7i","3")=2+7i
See Also
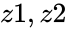 are the complex numbers is of the form
are the complex numbers is of the form 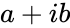
 &
&  are the real numbers.
are the real numbers.  imaginary unit .
imaginary unit .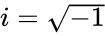 .
. and
and 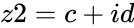 .
.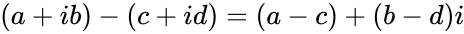 where
where 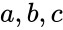 and
and 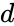 are real numbers.
are real numbers.