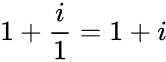Difference between revisions of "Manuals/calci/IMDIV"
Jump to navigation
Jump to search
| Line 19: | Line 19: | ||
**<math>ComplexNumber1</math> and <math>ComplexNumber2</math> are in the form of a+bi. | **<math>ComplexNumber1</math> and <math>ComplexNumber2</math> are in the form of a+bi. | ||
*For e.g.,IMDIV("3+2i","3-2i") | *For e.g.,IMDIV("3+2i","3-2i") | ||
| + | |||
| + | {{#ev:youtube|2I89nee0Gmc|280|center|ImDiv}} | ||
==Examples== | ==Examples== | ||
Revision as of 04:33, 25 June 2014
IMDIV(ComplexNumber1,ComplexNumber2)
- and are in the form of a+bi.
Description
- This function gives the division of two complex numbers.
- This function used to remove the (imaginary unit) from the denominator.
- and are in the form of and , where & are real numbers is the imaginary unit, .
- Let z1 and z2 are the two Complex Numbers.
- To do the division of complex number we have follow the steps:
step 1: Write the complex number in the fraction form. step 2: Find the conjugate of the denominator. step 3: Multiply the numerator and denominator with conjugate.
- .
- To find the Conjugate of a Complex Number we can use the function IMCONJUGATE.
ZOS Section
- The syntax is to calculate the IMDIV in ZOS is .
- and are in the form of a+bi.
- For e.g.,IMDIV("3+2i","3-2i")
Examples
- IMDIV("4+2i","3-i") = = (because ) =
- IMDIV("3-5i,2-6i") = 0.9+0.2i
- IMDIV("5","2+3i") = 0.769-1.153i
- IMDIV("1+i","2") = 0.5+0.5i
See Also
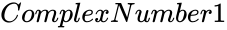 and
and 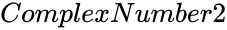 are in the form of a+bi.
are in the form of a+bi. (imaginary unit) from the denominator.
(imaginary unit) from the denominator.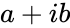 and
and 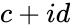 , where
, where 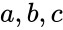 &
& 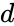 are real numbers
are real numbers 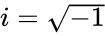 .
.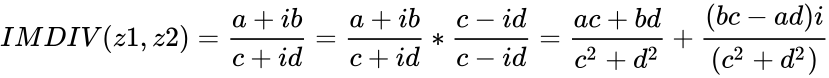 .
.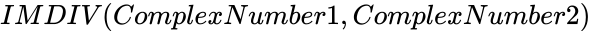 .
.
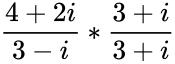 =
= 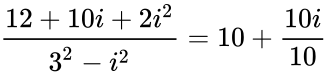 (because
(because 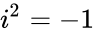 ) =
) =