Difference between revisions of "Manuals/calci/IMDIV"
Jump to navigation
Jump to search
| Line 23: | Line 23: | ||
==Examples== | ==Examples== | ||
| − | #IMDIV("4+2i","3-i") =<math>\frac{4+2i}{3-i}*\frac{3+i}{3+i}</math> = <math>\frac{12+10i+2i^2}{3^2-i^2} = 10+\frac{10i}{10}</math> (because <math>i^2=-1</math>) = <math> 1+\frac{i}{1} = 1+ | + | #IMDIV("4+2i","3-i") =<math>\frac{4+2i}{3-i}*\frac{3+i}{3+i}</math> = <math>\frac{12+10i+2i^2}{3^2-i^2} = 10+\frac{10i}{10}</math> (because <math>i^2=-1</math>) = <math> 1+\frac{i}{1} = 1+1i </math> |
#IMDIV("3-5i,2-6i") = 0.9+0.2i | #IMDIV("3-5i,2-6i") = 0.9+0.2i | ||
| − | #IMDIV("5","2+3i") = 0. | + | #IMDIV("5","2+3i") = 0.7692307692307693 + -1.1538461538461537i |
#IMDIV("1+i","2") = 0.5+0.5i | #IMDIV("1+i","2") = 0.5+0.5i | ||
Revision as of 23:21, 26 March 2015
IMDIV(ComplexNumber1,ComplexNumber2)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ComplexNumber1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ComplexNumber2} are in the form of a+bi.
Description
- This function gives the division of two complex numbers.
- This function used to remove the (imaginary unit) from the denominator.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ComplexNumber1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ComplexNumber2} are in the form of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a+ib} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c+id} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a,b,c} & Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d} are real numbers Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} is the imaginary unit, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=\sqrt{-1}} .
- Let z1 and z2 are the two Complex Numbers.
- To do the division of complex number we have follow the steps:
step 1: Write the complex number in the fraction form. step 2: Find the conjugate of the denominator. step 3: Multiply the numerator and denominator with conjugate.
- .
- To find the Conjugate of a Complex Number we can use the function IMCONJUGATE.
ZOS Section
- The syntax is to calculate the IMDIV in ZOS is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IMDIV(ComplexNumber1,ComplexNumber2)}
.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ComplexNumber1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ComplexNumber2} are in the form of a+bi.
- For e.g.,IMDIV("3+2i","3-2i")
Examples
- IMDIV("4+2i","3-i") =Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4+2i}{3-i}*\frac{3+i}{3+i}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{12+10i+2i^2}{3^2-i^2} = 10+\frac{10i}{10}} (because Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^2=-1} ) = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1+\frac{i}{1} = 1+1i }
- IMDIV("3-5i,2-6i") = 0.9+0.2i
- IMDIV("5","2+3i") = 0.7692307692307693 + -1.1538461538461537i
- IMDIV("1+i","2") = 0.5+0.5i
See Also
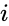 (imaginary unit) from the denominator.
(imaginary unit) from the denominator.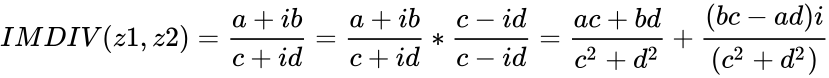 .
.