Difference between revisions of "Manuals/calci/CARTESIANPRODUCTWITHOUTFLATTEN"
Jump to navigation
Jump to search
| Line 33: | Line 33: | ||
| 19 || 23 | | 19 || 23 | ||
|} | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=NnEkVooAsxk|280|center|CARTESIAN PRODUCT}} | ||
==See Also== | ==See Also== | ||
Latest revision as of 14:58, 10 December 2018
CARTESIANPRODUCTWITHOUTFLATTEN (GivenSet1,GivenSet2)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle GivenSet1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle GivenSet2} are the set of numbers to find product.
Description
- This function shows the Cartesian product of two sets.
- Cartesian product is the product of two sets.
- The product of set X and set Y is the set that contains all ordered pairs ( x, y ) for which x belongs to X and y belongs to Y.
- In Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle CARTESIANPRODUCTWITHOUTFLATTEN(GivenSet1,GivenSet2)} ,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Givenset1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Givenset2} are two set of real numbers with a pair of numbers.
- Consider two sets Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \llcorner A } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \llcorner B } .
- The Cartesian product of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \llcorner A } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \llcorner B } are denoted by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \llcorner AXB } is the set of all ordered pairs Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \llcorner (a,b) } such that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a \in A} and .
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \llcorner AXB} = {Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a,b)|a \in A,b \in B} }
Examples
1.CARTESIANPRODUCTWITHOUTFLATTEN([10,13,19],[-5,8,23])
| 10 | -5 |
| 10 | 8 |
| 10 | 23 |
| 13 | -5 |
| 13 | 8 |
| 13 | 23 |
| 19 | -5 |
| 19 | 8 |
| 19 | 23 |
Related Videos
See Also
References
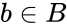 .
.