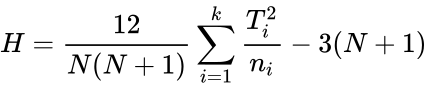KRUSKALWALLISTEST
Jump to navigation
Jump to search
KRUSKALWALLISTEST(SampleDataByGroup, Confidencelevel, Logicalvalue)
- is the set of values to find the test statistic.
- is the value between 0 and 1.
- is either TRUE or FALSE.
DESCRIPTION
- This function gives the test statistic value of the Kruskal Wallis test.
- It is one type of Non parametric test.
- It is a logical extension of the Wilcoxon-Mann-Whitney Test.
- The parametric equivalent of the Kruskal-Wallis test is the one-way analysis of variance (ANOVA).
- This test is used for comparing more than two sample that are independent or not related.
- It is used to test the null hypothesis that all populations have identical distribution functions against the alternative hypothesis that at least two of the samples differ only with respect to Median.
- Kruskal–Wallis is also used when the examined groups are of unequal size.
- When the Kruskal-Wallis test leads to significant results, then at least one of the samples is different from the other samples.
- The test does not identify where the differences occur or how many differences actually occur.
- Since it is a non-parametric method, the Kruskal–Wallis test does not assume a normal distribution of the residuals, unlike the analogous one-way analysis of variance.
- However, the test does assume an identically shaped and scaled distribution for each group, except for any difference in medians.
The Kruskal Wallis test data are having the following properties:
- The data points must be independent from each other.
- The distributions do not have to be normal and the variances do not have to be equal.
- The data points must be more than five per sample.
- All individuals must be selected at random from the population.
- All individuals must have equal chance of being selected.
- Sample sizes should be as equal as possible but some differences are allowed.
Steps for Kruskal Wallis Test:
- Define Null and Alternative Hypotheses:
- Null Hypotheses: There is no difference between the conditions.
- Alternative Hypotheses: There is a difference between the conditions.
- State Alpha: Alpha=0.05.
- Calculate degrees of freedom: df = k – 1, where k = number of groups.
- State Decision Rule: From the Chi squared table calculate the critical value.
Suppose the is greater than the critical value then reject the null hypothesis:
- Calculate the Test Statistic
- State Results: In this step we have to take a decision of null hypothesis either accept or reject depending on the critical value table.
- State Conclusion: To be significant, our obtained H has to be equal to or LESS than this critical value.
EXAMPLE
| A | B | C | |
|---|---|---|---|
| 1 | 46 | 44 | 26 |
| 2 | 32 | 31 | 49 |
| 3 | 42 | 25 | 33 |
| 4 | 45 | 22 | 19 |
| 5 | 37 | 30 | 31 |
| 6 | 44 | 30 | 38 |
| 7 | 38 | 32 | 44 |
| 8 | 47 | 19 | 50 |
| 9 | 49 | 40 | |
| 10 | 41 |
=KRUSKALWALLISTEST([A1:A10, B1:B9, C1:C8], 0.05, true)
| GROUP-0 | GROUP-1 | GROUP2 |
|---|---|---|
| 46 | 44 | 26 |
| 32 | 31 | 49 |
| 42 | 25 | 33 |
| 45 | 22 | 19 |
| 45 | 22 | 19 |
| 37 | 30 | 31 |
| 44 | 30 | 38 |
| 47 | 19 | 50 |
| 49 | 40 | undefined |
| 41 | undefined | undefined |
| GROUP-0 | GROUP-1 | GROUP-2 |
|---|---|---|
| 23 | 20 | 5 |
| 10.5 | 8.5 | 25.5 |
| 18 | 4 | 12 |
| 22 | 3 | 1.5 |
| 13 | 6.5 | 8.5 |
| 20 | 6.5 | 14.5 |
| 14.5 | 10.5 | 20 |
| 24 | 1.5 | 27 |
| 25.5 | 16 | undefined |
| 17 | undefined | undefined |
| GROUP-0 | GROUP-1 | GROUP-2 | |
|---|---|---|---|
| SUM OF RANKS | 187.5 | 76.5 | 114 |
| GROUP SIZE | 10 | 9 | 8 |
| R2/N | 3515.625 | 620.5 | 1624.5 |
| TOTALRANKSUM | 378 | ||
| TOTAL GROUP SIZE | 27 | ||
| TOTAL R2/N | 5790.375 | ||
| H | 7.910714285714278 | ||
| DF | 2 | ||
| P-VALUE | 0.019151827389727316 | ||
| A | 0.05 |
COMPARISON WITH OTHER SOFTWARE
Conduct Kruskal-Wallis test for the data in the range B2:D11.
Related Videos
See Also
References
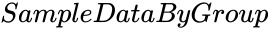 is the set of values to find the test statistic.
is the set of values to find the test statistic.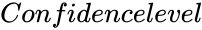 is the value between 0 and 1.
is the value between 0 and 1.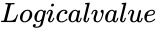 is either TRUE or FALSE.
is either TRUE or FALSE.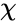 is greater than the critical value then reject the null hypothesis:
is greater than the critical value then reject the null hypothesis: