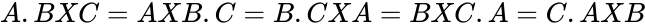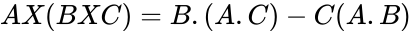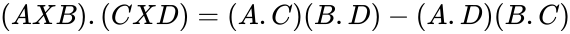Manuals/calci/DYADIC
DYADIC(a,b)
OR VECTORDIRECTPRODUCT (a,b)
- and any two set of values.
Description
- This function shows the Vector Direct product.
- The third type of vector multiplication is called the direct product, and is written AB.
- In , and are the two vectors.
- Multiplying one vector by another under the direct product gives a tensor result.
- The rectangular components of the direct product may be found by matrix multiplication: one multiplies the column vector A by the transpose of B, which gives a 3X3 matrix:
= =
- The direct product is non-commutative .
- A few vector product identities are of interest:
Examples
- DYADIC([1,2,3],[8,7,6]) = 40
- VECTORDIRECTPRODUCT([14,17,20],[22,26,5]) = 850
- VECTORDIRECTPRODUCT([2.7,3.9,10.2],[14.5,19,-4]) = 72.45
- DYADIC([-8,-4,2],[10,-45,67]) = 234
Related Videos
See Also
References
 and
and  any two set of values.
any two set of values.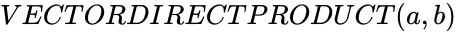 ,
, 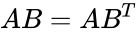 =
=
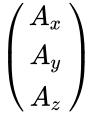
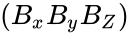 =
=
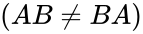 .
.