Difference between revisions of "Manuals/calci/SQRTPI"
Jump to navigation
Jump to search
| (4 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''SQRTPI( | + | <div style="font-size:30px">'''SQRTPI(Multiplier)'''</div><br/> |
| − | *<math> | + | *<math>Multiplier</math> is any number. |
| + | **SQRTPI(), returns the square root of (number * pi) | ||
==Description== | ==Description== | ||
*This function gives the square root of <math>(pi*n)</math>. | *This function gives the square root of <math>(pi*n)</math>. | ||
*The <math> pi</math> is a mathematical constant with a value approximate to 3.14159. | *The <math> pi</math> is a mathematical constant with a value approximate to 3.14159. | ||
| − | *In <math> SQRTPI( | + | *In <math> SQRTPI(Multiplier)</math>, <math>Multiplier</math> is the number by which <math> pi </math> is multiplied. When we are omitting the value of <math> Multiplier</math>, then it will consider the value <math>Multiplier=1</math>. |
*<math> PI()</math> is denoted by the Greek letter <math> \pi</math>. | *<math> PI()</math> is denoted by the Greek letter <math> \pi</math>. | ||
*<math> \pi </math> is a transcendental number and irrational number. | *<math> \pi </math> is a transcendental number and irrational number. | ||
*Being an irrational number, <math> \pi </math> cannot be expressed exactly as a ratio of any two integers, but we can express as the fraction 22/7 is approximate to the <math> \pi </math> value, also no fraction can be its exact value. | *Being an irrational number, <math> \pi </math> cannot be expressed exactly as a ratio of any two integers, but we can express as the fraction 22/7 is approximate to the <math> \pi </math> value, also no fraction can be its exact value. | ||
| − | This function will give the result as error when <math> | + | This function will give the result as error when <math>Multiplier<0</math>. |
==Examples== | ==Examples== | ||
| Line 15: | Line 16: | ||
#=SQRTPI(0) = 0 | #=SQRTPI(0) = 0 | ||
#=SQRTPI(5) = 3.963327298 | #=SQRTPI(5) = 3.963327298 | ||
| − | #=SQRTPI(-2) = | + | #=SQRTPI(-2) = #N/A (MULTIPLIER > 0 REQUIRED) |
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|ujwQMYge0uY|280|center|SQRT}} | ||
==See Also== | ==See Also== | ||
| Line 23: | Line 28: | ||
==References== | ==References== | ||
[http://en.wikipedia.org/wiki/Square_root Square Root] | [http://en.wikipedia.org/wiki/Square_root Square Root] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 03:26, 10 June 2020
SQRTPI(Multiplier)
- is any number.
- SQRTPI(), returns the square root of (number * pi)
Description
- This function gives the square root of .
- The is a mathematical constant with a value approximate to 3.14159.
- In , is the number by which is multiplied. When we are omitting the value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Multiplier} , then it will consider the value Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Multiplier=1} .
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle PI()} is denoted by the Greek letter Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} .
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi } is a transcendental number and irrational number.
- Being an irrational number, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi } cannot be expressed exactly as a ratio of any two integers, but we can express as the fraction 22/7 is approximate to the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi } value, also no fraction can be its exact value.
This function will give the result as error when Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Multiplier<0}
.
Examples
- =SQRTPI(1) = 1.772453851
- =SQRTPI(0) = 0
- =SQRTPI(5) = 3.963327298
- =SQRTPI(-2) = #N/A (MULTIPLIER > 0 REQUIRED)
Related Videos
See Also
References
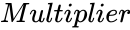 is any number.
is any number.
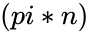 .
.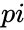 is a mathematical constant with a value approximate to 3.14159.
is a mathematical constant with a value approximate to 3.14159.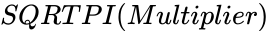 ,
,