Difference between revisions of "Manuals/calci/IMARGUMENT"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> <font color="#000000"><font face="Arial, sans-serif"><font size="2">'''IMARGUMENT'''</font></font><font face="Arial, sa...") |
|||
| (24 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''IMARGUMENT(Complexnumber)'''</div><br/> |
| + | *<math>Complexnumber</math> is of the form <math>z=x+iy</math>. | ||
| + | **IMARGUMENT(), returns the argument theta, an angle expressed in radians | ||
| − | < | + | ==Description== |
| + | *This function gives the principal value of an argument of a complex-valued expression <math>z</math>. | ||
| + | * i.e The angle from the positive axis to the line segment is called the Argument of a complex number. | ||
| + | *In this function angle value is in Radians. | ||
| + | *Here <math>IMARGUMENT(Complexnumber)</math>, Where Complexnumber in the form of <math>z=x+iy</math>. i.e <math>x</math> & <math>y</math> are the real numbers. | ||
| + | *<math>I</math> imaginary unit .<math>i=\sqrt{-1}</math>. | ||
| + | *An argument of the complex number <math>z = x + iy</math> is any real quantity <math>\phi</math> such that <math>z = x + i y</math> = <math>r cos(\phi) + i r sin(\phi)</math> for some positive real number <math>r</math>. | ||
| + | *Where <math>r = |z| = \sqrt{x^2+y^2}</math> and <math>\phi \in (-\pi,\pi]</math>. | ||
| + | *The argument of a complex number is calculated by <math>arg(z)= tan^{-1}(\frac{y}{x}) =\theta</math> in Radians. | ||
| + | *To change the Radian value to Degree we can use DEGREES function or we can multiply the answer with <math>\frac{180}{\pi}</math>. | ||
| + | *We can use [[Manuals/calci/COMPLEX| COMPLEX]] function to convert real and imaginary number in to a complex number. | ||
| − | </ | + | ==ZOS== |
| − | + | *The syntax is to calculate argument of a complex number in ZOS is <math>IMARGUMENT(Complexnumber)</math>. | |
| − | < | + | **<math>Complexnumber</math> is of the form <math>z=x+iy</math>. |
| + | *For e.g.,IMARGUMENT("6.72+1.5i") | ||
| + | {{#ev:youtube|oO4FgWYhIhw|280|center|Imargument}} | ||
| − | + | ==Examples== | |
| − | + | #IMARGUMENT("3-2i") = -0.5880026035475675 | |
| + | #IMARGUMENT("5+6i") = 0.8760580505981934 | ||
| + | #IMARGUMENT("2") = 0 | ||
| + | #IMARGUMENT("4i") = 1.5707963267948966 | ||
| + | #DEGREES(IMARGUMENT("2+2i")) = 45° | ||
| − | + | ==Related Videos== | |
| − | + | {{#ev:youtube|FwuPXchH2rA|280|center|Complex Number Analysis}} | |
| − | + | ==See Also== | |
| − | + | *[[Manuals/calci/IMAGINARY | IMAGINARY ]] | |
| − | + | *[[Manuals/calci/IMREAL | IMREAL]] | |
| + | *[[Manuals/calci/IMSUM | IMSUM ]] | ||
| − | + | ==References== | |
| + | *[http://mathworld.wolfram.com/ComplexArgument.html Complex Argument] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *[[Z_API_Functions | List of Main Z Functions]] | |
| − | + | *[[ Z3 | Z3 home ]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 03:18, 23 October 2020
IMARGUMENT(Complexnumber)
- is of the form .
- IMARGUMENT(), returns the argument theta, an angle expressed in radians
Description
- This function gives the principal value of an argument of a complex-valued expression .
- i.e The angle from the positive axis to the line segment is called the Argument of a complex number.
- In this function angle value is in Radians.
- Here Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IMARGUMENT(Complexnumber)} , Where Complexnumber in the form of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=x+iy} . i.e Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} & Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} are the real numbers.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I} imaginary unit .Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=\sqrt{-1}} .
- An argument of the complex number Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = x + iy} is any real quantity Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} such that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = x + i y} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r cos(\phi) + i r sin(\phi)} for some positive real number Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} .
- Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r = |z| = \sqrt{x^2+y^2}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi \in (-\pi,\pi]} .
- The argument of a complex number is calculated by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle arg(z)= tan^{-1}(\frac{y}{x}) =\theta} in Radians.
- To change the Radian value to Degree we can use DEGREES function or we can multiply the answer with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{180}{\pi}} .
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
ZOS
- The syntax is to calculate argument of a complex number in ZOS is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IMARGUMENT(Complexnumber)}
.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Complexnumber} is of the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=x+iy} .
- For e.g.,IMARGUMENT("6.72+1.5i")
Examples
- IMARGUMENT("3-2i") = -0.5880026035475675
- IMARGUMENT("5+6i") = 0.8760580505981934
- IMARGUMENT("2") = 0
- IMARGUMENT("4i") = 1.5707963267948966
- DEGREES(IMARGUMENT("2+2i")) = 45°
Related Videos
See Also
References
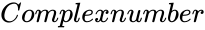 is of the form
is of the form 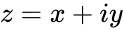 .
.
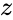 .
.