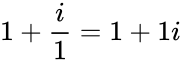Difference between revisions of "Manuals/calci/IMDIV"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''IMDIV( | + | <div style="font-size:30px">'''IMDIV()'''</div><br/> |
| − | * | + | *Parameters are in the form of a+bi. |
| + | **IMDIV(),returns the quotient of two complex numbers | ||
==Description== | ==Description== | ||
| Line 6: | Line 7: | ||
*This function gives the division of two complex numbers. | *This function gives the division of two complex numbers. | ||
*This function used to remove the <math>i</math> (imaginary unit) from the denominator. | *This function used to remove the <math>i</math> (imaginary unit) from the denominator. | ||
| − | * | + | *The two Parameters are in the form of <math>a+ib</math> and <math>c+id</math>, where <math>a,b,c</math> & <math>d</math> are real numbers <math>i</math> is the imaginary unit, <math>i=\sqrt{-1}</math>. |
*Let z1 and z2 are the two Complex Numbers. | *Let z1 and z2 are the two Complex Numbers. | ||
*To do the division of complex number we have follow the steps: | *To do the division of complex number we have follow the steps: | ||
| Line 16: | Line 17: | ||
==ZOS== | ==ZOS== | ||
| − | *The syntax is to calculate the IMDIV in ZOS is <math>IMDIV( | + | *The syntax is to calculate the IMDIV in ZOS is <math>IMDIV()</math>. |
| − | ** | + | **Parameters are in the form of a+bi. |
*For e.g.,IMDIV("3+2i","3-2i") | *For e.g.,IMDIV("3+2i","3-2i") | ||
Revision as of 15:23, 16 July 2018
IMDIV()
- Parameters are in the form of a+bi.
- IMDIV(),returns the quotient of two complex numbers
Description
- This function gives the division of two complex numbers.
- This function used to remove the (imaginary unit) from the denominator.
- The two Parameters are in the form of and , where & are real numbers is the imaginary unit, .
- Let z1 and z2 are the two Complex Numbers.
- To do the division of complex number we have follow the steps:
step 1: Write the complex number in the fraction form. step 2: Find the conjugate of the denominator. step 3: Multiply the numerator and denominator with conjugate.
- .
- To find the Conjugate of a Complex Number we can use the function IMCONJUGATE.
ZOS
- The syntax is to calculate the IMDIV in ZOS is .
- Parameters are in the form of a+bi.
- For e.g.,IMDIV("3+2i","3-2i")
Examples
- IMDIV("4+2i","3-i") = = (because ) =
- IMDIV("3-5i","2-6i") = 0.9+0.2i
- IMDIV("5","2+3i") = 0.7692307692307693 + -1.1538461538461537i
- IMDIV("1+i","2") = 0.5+0.5i
Related Videos
See Also
References
 (imaginary unit) from the denominator.
(imaginary unit) from the denominator.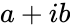 and
and 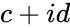 , where
, where 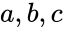 &
&  are real numbers
are real numbers 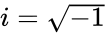 .
.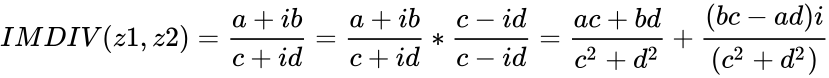 .
.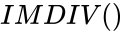 .
.
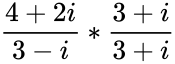 =
= 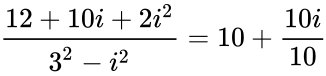 (because
(because 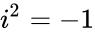 ) =
) =