Difference between revisions of "Manuals/calci/NORMSINV"
Jump to navigation
Jump to search
'
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> '''NORMSINV'''('''p''') '''Where p''' is a probability equivalent to the normal distribution. </div> ---- ...") |
|||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''NORMSINV(prob)'''</div><br/> |
| + | *<math>prob</math> prob is the probability value. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives the inverse of the standard normal cumulative distribution. | ||
| + | *In normal distribution formula, when the mean is zero and the standard deviation is 1 then it is called Standard normal distribution. | ||
| + | *If <math> NORMSDIST(x)=prob</math>, then <math>NORMSINV(prob)=x</math>. | ||
| + | *<math>NORMSINV</math> using the iterating method to find the value of x. | ||
| + | *Suppose the iteration has not converged after 100 searches, then the function gives the error result. | ||
| + | *In <math>NORMSINV(prob)</math>, where prob is the probability value of the standard normal cumulative distribution. | ||
| + | *This function will return the result as error when | ||
| + | 1.prob is nonnumeric. | ||
| + | 2.prob<0 or prob>1. | ||
| + | |||
| + | ==Examples== | ||
| + | #NORMSINV(0.9999975333)=4.567600 | ||
| + | #NORMSINV(0.00241)=-2.818823592 | ||
| + | #NORMSINV(1)=Null | ||
| + | #NORMSINV(0.00001)=-4.264890794 | ||
| + | |||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/NORMDIST | NORMDIST ]] | ||
| + | *[[Manuals/calci/NORMINV | NORMINV ]] | ||
| + | *[[Manuals/calci/NORMSDIST | NORMSDIST ]] | ||
| + | |||
| + | ==References== | ||
| + | |||
| + | |||
| + | |||
'''NORMSINV'''('''p''') | '''NORMSINV'''('''p''') | ||
Revision as of 03:36, 2 January 2014
NORMSINV(prob)
- prob is the probability value.
Description
- This function gives the inverse of the standard normal cumulative distribution.
- In normal distribution formula, when the mean is zero and the standard deviation is 1 then it is called Standard normal distribution.
- If , then .
- using the iterating method to find the value of x.
- Suppose the iteration has not converged after 100 searches, then the function gives the error result.
- In , where prob is the probability value of the standard normal cumulative distribution.
- This function will return the result as error when
1.prob is nonnumeric. 2.prob<0 or prob>1.
Examples
- NORMSINV(0.9999975333)=4.567600
- NORMSINV(0.00241)=-2.818823592
- NORMSINV(1)=Null
- NORMSINV(0.00001)=-4.264890794
See Also
References
NORMSINV(p)
Where p is a probability equivalent to the normal distribution.
It calculates the inverse of the standard normal cumulative distribution.
· For nonnumeric p ,NORMSINV shows error.
· When p< 0 or p> 1, NORMSINV displays error.
NORMSINV
Let’s see an example in (Column1 Row 1)
i.e.= NORMSINV (C1R1)
i.e.= NORMSINV (0.80879) is 0.8734
Syntax
Remarks
Examples
Description
| Column1 | Column2 | Column3 | Column4 | |||
| Row1 | 0.80879 | |||||
| Row2 | 0.8734460503371548 | |||||
| Row3 | ||||||
| Row4 | ||||||
| Row5 | ||||||
| Row6 |
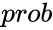 prob is the probability value.
prob is the probability value.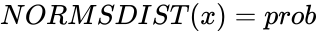 , then
, then 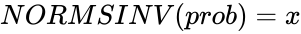 .
.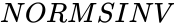 using the iterating method to find the value of x.
using the iterating method to find the value of x.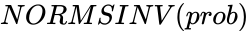 , where prob is the probability value of the standard normal cumulative distribution.
, where prob is the probability value of the standard normal cumulative distribution.