Difference between revisions of "Manuals/calci/NORMDIST"
Jump to navigation
Jump to search
| Line 7: | Line 7: | ||
*This distribution is the continuous probability distribution.It is also called Gaussian distribution. | *This distribution is the continuous probability distribution.It is also called Gaussian distribution. | ||
*In <math> NORMDIST(x,m,sd,cu) ,x</math> is the value of the function,<math> m</math> is the arithmetic mean of the distribution, <math>sd</math> is the standard deviation of the distribution and <math>cu</math> is the logical value that indicating the form of the function. | *In <math> NORMDIST(x,m,sd,cu) ,x</math> is the value of the function,<math> m</math> is the arithmetic mean of the distribution, <math>sd</math> is the standard deviation of the distribution and <math>cu</math> is the logical value that indicating the form of the function. | ||
| − | *Suppose cu is TRUE, this function gives the cumulative distribution, and it is FALSE, this function | + | *Suppose cu is TRUE, this function gives the cumulative distribution, and it is FALSE, this function gives the probability mass function. |
| − | *The equation for the normal distribution is: <math> f(x,\mu,\sigma)=\frac{1}{\sigma \sqrt{2\pi}}.e^-\left({\frac{(x-\mu)^2}{2\sigma^2}}\right)</math> | + | *The equation for the normal distribution is: <math> f(x,\mu,\sigma)=\frac{1}{\sigma \sqrt{2\pi}}.e^-\left({\frac{(x-\mu)^2}{2\sigma^2}}\right)</math> where <math>\mu</math> is the mean of the distribution,<math>\sigma</math> is the standard deviation of the distribution. |
*In this formula, Suppose <math>\mu</math> = 0 and <math>\sigma</math>= 1, then the distribution is called the standard normal distribution or the unit normal distribution. | *In this formula, Suppose <math>\mu</math> = 0 and <math>\sigma</math>= 1, then the distribution is called the standard normal distribution or the unit normal distribution. | ||
*This function will return the result as error when any one of the argument is nonnumeric and sd<=0. | *This function will return the result as error when any one of the argument is nonnumeric and sd<=0. | ||
when cu is TRUE , this formula is the integral from -infinity to x and cu is FALSE , we can use the same formula. | when cu is TRUE , this formula is the integral from -infinity to x and cu is FALSE , we can use the same formula. | ||
| + | |||
| + | |||
| + | ==Examples== | ||
| + | #NORMDIST(37,29,2.1,FALSE)=0.000134075 | ||
| + | #NORMDIST(37,29,2.1,TRUE)=0.99993041384 | ||
| + | #NORMDIST(10.75,17.4,3.2,TRUE)=0.01884908749 | ||
| + | #NORMDIST(10.75,17.4,3.2,FALSE)=0.014387563 | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/NORMINV | NORMINV ]] | ||
| + | *[[Manuals/calci/NORMSDIST | NORMSDIST ]] | ||
| + | *[[Manuals/calci/NORMSINV | NORMSINV ]] | ||
| + | |||
| + | ==References== | ||
Revision as of 03:35, 1 January 2014
NORMDIST(x,m,sd,cu)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is the value,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} is the mean,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle sd} is the standard deviation and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cu} is the logical value like TRUE or FALSE.
Description
- This function gives the normal distribution for the particular mean and standard deviation.
- Normal distribution is the function that represents the distribution of many random variables as a symmetrical bell-shaped graph.
- This distribution is the continuous probability distribution.It is also called Gaussian distribution.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NORMDIST(x,m,sd,cu) ,x} is the value of the function,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} is the arithmetic mean of the distribution, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle sd} is the standard deviation of the distribution and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cu} is the logical value that indicating the form of the function.
- Suppose cu is TRUE, this function gives the cumulative distribution, and it is FALSE, this function gives the probability mass function.
- The equation for the normal distribution is: where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} is the mean of the distribution,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} is the standard deviation of the distribution.
- In this formula, Suppose Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} = 0 and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} = 1, then the distribution is called the standard normal distribution or the unit normal distribution.
- This function will return the result as error when any one of the argument is nonnumeric and sd<=0.
when cu is TRUE , this formula is the integral from -infinity to x and cu is FALSE , we can use the same formula.
Examples
- NORMDIST(37,29,2.1,FALSE)=0.000134075
- NORMDIST(37,29,2.1,TRUE)=0.99993041384
- NORMDIST(10.75,17.4,3.2,TRUE)=0.01884908749
- NORMDIST(10.75,17.4,3.2,FALSE)=0.014387563
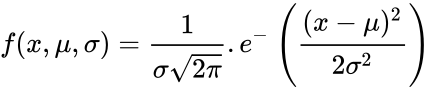 where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu}
is the mean of the distribution,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma}
is the standard deviation of the distribution.
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu}
is the mean of the distribution,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma}
is the standard deviation of the distribution.