Difference between revisions of "Manuals/calci/NORMINV"
Jump to navigation
Jump to search
| (6 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''NORMINV( | + | <div style="font-size:30px">'''NORMINV (Probability,Mean,StandardDeviation)'''</div><br/> |
| − | *<math> | + | *<math>Probability</math> is the probability corresponding to the Normal Distribution. |
| + | *<math>Mean</math> is the Mean value. | ||
| + | *<math>StandardDeviation</math> is the Standard Deviation. | ||
| + | **NORMINV(),returns the inverse of the normal cumulative distribution. | ||
==Description== | ==Description== | ||
*This function gives the inverse of the Normal Cumulative Distribution for the particular Mean and Standard Deviation. | *This function gives the inverse of the Normal Cumulative Distribution for the particular Mean and Standard Deviation. | ||
| − | *If <math>NORMDIST( | + | *If <math>NORMDIST (Number,Mean,StandardDeviation,Cumulative,accuracy)=Probability</math>, then <math>NORMINV (Probability,Mean,StandardDeviation)=Number</math>. |
| − | *<math>NORMINV</math> using the iterating method to find the value of | + | *<math>NORMINV</math> using the iterating method to find the value of a Number. |
*Suppose the iteration has not converged after 100 searches, then the function gives the error result. | *Suppose the iteration has not converged after 100 searches, then the function gives the error result. | ||
| − | *In <math>NORMINV( | + | *In <math>NORMINV (Probability,Mean,StandardDeviation)</math>, where <math>Probability</math> is the corresponding probability of the Normal Distribution, <math>Mean</math> is the Arithmetic Mean of the Normal Distribution and <math>StandardDeviation</math> is the Standard Deviation of the Normal Distribution. |
*This function will return the result as error when | *This function will return the result as error when | ||
1.any one of the argument is non-numeric | 1.any one of the argument is non-numeric | ||
| − | 2.Suppose | + | 2.Suppose Probability<0 or Probability>1 |
| − | 3. | + | 3. StandardDeviation<=0. |
| − | *If | + | *If Mean=0 and StandardDeviation=1, NORMINV uses the Standard Normal Distribution. |
==Examples== | ==Examples== | ||
| Line 18: | Line 21: | ||
#=NORMINV(0.998742,5.4,2.3) = 12.349244172 | #=NORMINV(0.998742,5.4,2.3) = 12.349244172 | ||
#=NORMINV(1,7.2,2.3) = NULL | #=NORMINV(1,7.2,2.3) = NULL | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|jMFs_1gmqWw|280|center|NORMDIST AND NORMINV}} | ||
==See Also== | ==See Also== | ||
| Line 26: | Line 33: | ||
==References== | ==References== | ||
[http://en.wikipedia.org/wiki/Normal_distribution Normal distribution ] | [http://en.wikipedia.org/wiki/Normal_distribution Normal distribution ] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 16:21, 10 August 2018
NORMINV (Probability,Mean,StandardDeviation)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Probability} is the probability corresponding to the Normal Distribution.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Mean} is the Mean value.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle StandardDeviation}
is the Standard Deviation.
- NORMINV(),returns the inverse of the normal cumulative distribution.
Description
- This function gives the inverse of the Normal Cumulative Distribution for the particular Mean and Standard Deviation.
- If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NORMDIST (Number,Mean,StandardDeviation,Cumulative,accuracy)=Probability} , then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NORMINV (Probability,Mean,StandardDeviation)=Number} .
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NORMINV} using the iterating method to find the value of a Number.
- Suppose the iteration has not converged after 100 searches, then the function gives the error result.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NORMINV (Probability,Mean,StandardDeviation)} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Probability} is the corresponding probability of the Normal Distribution, is the Arithmetic Mean of the Normal Distribution and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle StandardDeviation} is the Standard Deviation of the Normal Distribution.
- This function will return the result as error when
1.any one of the argument is non-numeric 2.Suppose Probability<0 or Probability>1 3. StandardDeviation<=0.
- If Mean=0 and StandardDeviation=1, NORMINV uses the Standard Normal Distribution.
Examples
- =NORMINV(0.01884908749,17.4,3.2) = 10.750011
- =NORMINV(0.998742,5.4,2.3) = 12.349244172
- =NORMINV(1,7.2,2.3) = NULL
Related Videos
See Also
References
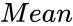 is the Arithmetic Mean of the Normal Distribution and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle StandardDeviation}
is the Standard Deviation of the Normal Distribution.
is the Arithmetic Mean of the Normal Distribution and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle StandardDeviation}
is the Standard Deviation of the Normal Distribution.