Difference between revisions of "Manuals/calci/NORMINV"
Jump to navigation
Jump to search
| (3 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
*<math>Mean</math> is the Mean value. | *<math>Mean</math> is the Mean value. | ||
*<math>StandardDeviation</math> is the Standard Deviation. | *<math>StandardDeviation</math> is the Standard Deviation. | ||
| + | **NORMINV(),returns the inverse of the normal cumulative distribution. | ||
==Description== | ==Description== | ||
*This function gives the inverse of the Normal Cumulative Distribution for the particular Mean and Standard Deviation. | *This function gives the inverse of the Normal Cumulative Distribution for the particular Mean and Standard Deviation. | ||
| − | *If <math>NORMDIST (Number,Mean,StandardDeviation,Cumulative,accuracy)=Probability</math>, then <math>NORMINV (Probability,Mean,StandardDeviation)= | + | *If <math>NORMDIST (Number,Mean,StandardDeviation,Cumulative,accuracy)=Probability</math>, then <math>NORMINV (Probability,Mean,StandardDeviation)=Number</math>. |
| − | *<math>NORMINV</math> using the iterating method to find the value of | + | *<math>NORMINV</math> using the iterating method to find the value of a Number. |
*Suppose the iteration has not converged after 100 searches, then the function gives the error result. | *Suppose the iteration has not converged after 100 searches, then the function gives the error result. | ||
*In <math>NORMINV (Probability,Mean,StandardDeviation)</math>, where <math>Probability</math> is the corresponding probability of the Normal Distribution, <math>Mean</math> is the Arithmetic Mean of the Normal Distribution and <math>StandardDeviation</math> is the Standard Deviation of the Normal Distribution. | *In <math>NORMINV (Probability,Mean,StandardDeviation)</math>, where <math>Probability</math> is the corresponding probability of the Normal Distribution, <math>Mean</math> is the Arithmetic Mean of the Normal Distribution and <math>StandardDeviation</math> is the Standard Deviation of the Normal Distribution. | ||
*This function will return the result as error when | *This function will return the result as error when | ||
1.any one of the argument is non-numeric | 1.any one of the argument is non-numeric | ||
| − | 2.Suppose | + | 2.Suppose Probability<0 or Probability>1 |
| − | 3. | + | 3. StandardDeviation<=0. |
| − | *If | + | *If Mean=0 and StandardDeviation=1, NORMINV uses the Standard Normal Distribution. |
==Examples== | ==Examples== | ||
Latest revision as of 16:21, 10 August 2018
NORMINV (Probability,Mean,StandardDeviation)
- is the probability corresponding to the Normal Distribution.
- is the Mean value.
- is the Standard Deviation.
- NORMINV(),returns the inverse of the normal cumulative distribution.
Description
- This function gives the inverse of the Normal Cumulative Distribution for the particular Mean and Standard Deviation.
- If , then .
- using the iterating method to find the value of a Number.
- Suppose the iteration has not converged after 100 searches, then the function gives the error result.
- In , where is the corresponding probability of the Normal Distribution, is the Arithmetic Mean of the Normal Distribution and is the Standard Deviation of the Normal Distribution.
- This function will return the result as error when
1.any one of the argument is non-numeric 2.Suppose Probability<0 or Probability>1 3. StandardDeviation<=0.
- If Mean=0 and StandardDeviation=1, NORMINV uses the Standard Normal Distribution.
Examples
- =NORMINV(0.01884908749,17.4,3.2) = 10.750011
- =NORMINV(0.998742,5.4,2.3) = 12.349244172
- =NORMINV(1,7.2,2.3) = NULL
Related Videos
See Also
References
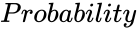 is the probability corresponding to the Normal Distribution.
is the probability corresponding to the Normal Distribution.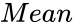 is the Mean value.
is the Mean value.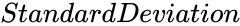 is the Standard Deviation.
is the Standard Deviation.
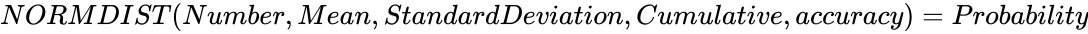 , then
, then 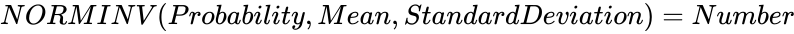 .
. using the iterating method to find the value of a Number.
using the iterating method to find the value of a Number.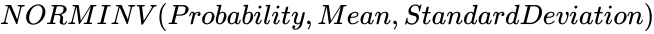 , where
, where